(По материалам компании Alcatel - L.F. Mojoli U. Mengali “Propagation in line of sight radio links”)

1. ВВЕДЕНИЕ

На распространение радиоволн вблизи поверхности земли влияют вертикальные изменения в показателе преломления атмосферы. По причине рефракции радиоволны проходят по изогнутым путям в вертикальной плоскости. Величина кривизны пути меняется со временем из-за изменения давления, температуры и влажности. При нормальных условиях распространения траектория радиолуча изгибается так, что имеет форму дуги, выгнутой к земле, и радиогоризонт расширяется. Однако, когда градиент рефракции увеличивается, траектория луча изгибается в обратную сторону, что приводит к уменьшению радиогоризонта. Когда трасса радиосвязи проходит низко над поверхностью земли могут появиться дополнительные дифракционные потери на наземных препятствиях. Например, если ось луча только касается препятствия, затухание сигнала может составить от 6 до 20 дБ, в зависимости от типа поверхности. В критических случаях препятствие может фактически закрывать весь радиолуч. В этом случае пропадает прямая видимость между передающей и приемной антеннами и принимаемый сигнал может стать настолько слабым, что РРЛ перестанет функционировать.

Одна из самых главных задач при проектировании радиорелейной линии связи - выбрать высоты антенн так, чтобы потеря прямой видимости между ними было чрезвычайно редким событием.

Для этого необходимо иметь точную информацию как о профиле трассы так и об отклонении радиолуча по причине изменения метереологических условий на трассе. Необходимо гарантировать достаточный просвет для самого худшего случая (самого низкого луча ) на трассе. Это может быть достигнуто соответствующим выбором высот антенн, которые, однако не могут быть больше чем фактически необходимые как по экономическим причинам, так и по причине ( на трассах со значительными отражениями от земной поверхности) заметного увеличения риска межсимвольной интерференции и искажения сигнала.

В данной главе даются критерии прямой видимости, которые позволяют проектировщику ограничить высоты подвеса антенн минимумом, совместимым с незначительной вероятностью потери видимости на трассе. Данные подходы применимы к различным климатическим условиям и основаны на данных, полученных из [1-3].

Глава имеет следующую структуру. В следующем разделе мы будем обсуждать распространение радиоволн в идеальной атмосфере, которая имеет постоянный градиент рефракции G. Эта модель ведет к важному понятию - “эквивалентный радиус”. Соответственно радиоволны рассматриваются как распространяющиеся прямолинейно над фиктивной земной поверхностью радиуса KR, где R представляет фактический земной радиус, а K называется эффективный радиус-фактор, который определяется следующим выражением:

(1)

где G - в единицах/километр (N-units/km).

В разделе 3 мы расширим эту модель, чтобы принять во внимание тот факт, что в реальности градиент рефракции не одинаковый на различных участках трассы. Поэтому необходимо ввести понятие эквивалентного градиента рефракции G_e который является статистической величиной - пространственным средним из различных градиентов на протяжении длинны трассы, и чьё распределение возможно оценить для разных трасс. Зная это распределение представляется возможным оценить вероятность появления минимальных (нежелательных) значений K.

Потери по причине дифракции обсуждаются в разделе 4 с использованием понятий чистоты зон Френеля для некоторых типов препятствий. В заключительном 5-ом разделе даются некоторые практические рекомендации для определения высот антенн.

2. ВЛИЯНИЕ АТМОСФЕРЫ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН.

Одним из самых главных факторов, влияющих на распространение радиоволн в атмосфере является изменение коэффициента преломления n с высотой. Это происходит по причине зависимости n от давления, температуры и влажности, которые изменяются с высотой. Для частот вплоть до 30 ГГц коэффициент преломления определяется по формуле [4]:

где p - атмосферное давление (mb);

e - порционное давление водяных паров (mb);

T - абсолютная температура (K).

Так как n немногим отличается от единицы удобнее работать с величиной

(2)

Например, коэффициент преломления в 350 N- единиц соответствует значению n=1.000350.

В общем случае ось радиолуча может проходить в сотни метрах от поверхности земли. Согласно [5] на таких высотах в смешанных слоях атмосферы коэффициент преломления уменьшается одинаково с высотой h, и, следовательно градиент

(3)

постоянен при изменении h.

Но это не значит что G неизменен во времени.

 

 

 

 

 

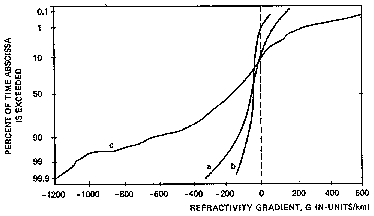
Рис.1 Распределение градиента рефракции

1. Trappes (Франция), умеренный климат
2. Ostersund (Швеция), северный климат
3. Dakar (Синегал), тропический климат

С другой стороны G сильно зависит от типа климата. На рис.1 показаны экспериментально полученные кривые распределения G в трех различных климатических зонах. Не трудно заметить, что среднее значение G для умеренного климата составляет -40 N ед/км.

Согласно предположению о постоянном градиенте в [5-6] показано, что радиолуч можно представить как дугу окружности радиусом r, которая выражена через коэффициент преломления n следующим образом:

(4)

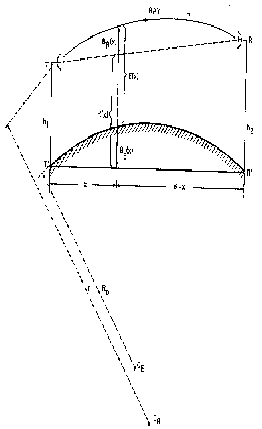
На рис.2 показана геометрия радиолуча. Кривизна земли представлена дугой окружности радиусом R₀, в то время как траектория радиолуча - дуга окружности радиусом r. Пусть h1 и h2 - высоты антенн над линией T’R’ и H(x) - просвет оси, тогда:

(5)

Высота луча над поверхностью земли может быть выражена как

(6)

где B_R и B_E - соответственно выпуклость луча и выпуклость земли в рассматриваемой точке. Они легко вычисляются если принять во внимание то, что обычно дуги T’R’ и TR могут быть аппроксимированы параболами [6]:

(7)

Рис.2 Геометрическая модель, иллюстрирующая изгибание луча.

(8)

Часто бывает удобно использовать геометрическую трансформацию рис.2, чтобы получить ситуацию, при которой прямой радиолуч распространяется над земной поверхностью с эквивалентным радиусом KR₀, или наоборот, луч с эффективным радиусом KR₀ распространяется над плоской земной поверхностью. В любом из этих случаев значение K, называемое “эффективным радиус - фактором” таково, что высота луча (просвет) E(x) над землёй имеет ту же функциональную зависимость от расстояния x как и на первоначальном рисунке (рис.2).

 

 

 

 

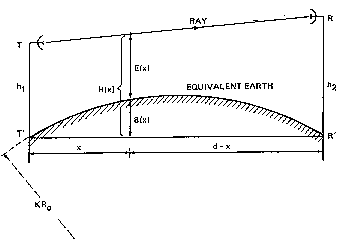
Рис.3 Профиль пролета на эквивалентной земной поверхности.

На рис.3 показана модель с эквивалентной земной поверхностью. Высота луча:

(9)

где B(x) - эквивалентная кривизна земли, которая представляется как:

(10)

Исходя из того, что правые части выражений (6) и (9) должны быть одинаковыми, имеем:

Или, используя (7)-(8) и (10):

(11)

Данное соотношение определяет K как функцию от R₀ и r.

Подобным образом можно иметь дело с моделью плоской земной поверхности. На рис.4 показано как кривизну земли можно отнести к кривизне луча. Так как земная поверхность становится плоской, то радиолуч принимает ту же форму с той же кривизной (но с противоположным знаком) эквивалентную кривизне земли на рис.3.

При рассмотрении рис.3, рис.4 и выражения (10) становится понятным, что высота луча над земной поверхностью зависит от значения K. С другой стороны K зависит от r (11) и следовательно от градиента коэффициента преломления, как показано на (4). Простое соотношение между K и градиентом рефракции G может быть получено следующим образом. Из (2) и (3) мы имеем:

Следовательно, из (4):

(12)

 

 

 

 

 

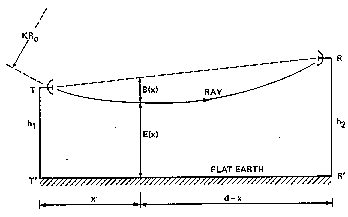
Рис.4 Профиль пролета на плоской земной поверхности.

 

 

 

 

 

 

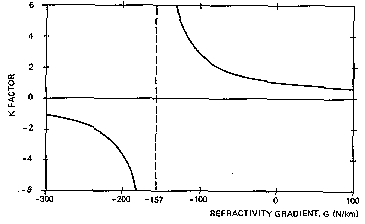
Рис.5 Эффективный радиус фактор как функция градиента рефракции

Теперь при подстановки (12) в (11) и приняв во внимание то, что радиус Земли равен км, получим:

(13)

где G в N-ед/км. Выражение (13) графически показано на рис.5.

Как было показано выше, в умеренном климате среднее значение G составляет около -40 N-ед/км, соответствующие этому значение K=4/3. Такие метереологические условия принимают за стандартные. Однако даже в условиях умеренного климата возможны значительные отклонения градиента G от среднего значения по причине изменения метереологических условий.

 

 

 

 

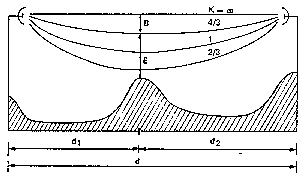
Рис.6 Изменение кривизны луча как функция K.

Эффект, получающийся в следствии этих изменений показан на рис.6. Видно, что на вершине холма просвет наименьший. Эта точка называется критическим препятствием. Пусть d1 и d2 - расстояния от критического препятствия до передатчика и приемника, тогда выпуклость луча определяется как (10):

(14)

При стандартных атмосферных условиях K=4/3. Когда K становится меньшим (как следствие увеличения G), тогда увеличивается кривизна луча, и, соответственно уменьшается просвет. И наоборот, при увеличении K уменьшается кривизна луча и в предельном случае при K=? луч становится прямой линией. Это происходит при G=157 (13). Меньшие значения G приводят к отрицательным значениям K, и соответствуют траектории луча, изогнутой вверх.

 

3. МИНИМАЛЬНОЕ ЗНАЧЕНИЕ K.

В предыдущем разделе было сделано предположение, что градиент G принимает одинаковые значения в различных точках трассы. Поскольку это очевидно грубое предположение (особенно на длинных пролетах) возникает вопрос - как проследить изменение траектории радиолуча при изменении градиента G вдоль трассы РРЛ. Эта проблема была обсуждена в [7] и были получены следующие результаты для установления критерия прямой видимости:

а) Фактическая траектория также приблизительно аппроксимируется дугой окружности с кривизной

(15)

где G_e - эквивалентный градиент рефракции;

б) G_e - среднее значение градиентов преломления G распределенных вдоль пролета;

в) G_e - случайная величина, распределенная по закону Гаусса на длинных пролетах. Пусть m и s - математическое ожидание и среднеквадратическое отклонение величины G, полученные из метереологических наблюдений на интересующем нас участке, тогда:

(16)

(17)

где d - длинна пролета, км; d₀=13.5 км. Приведенная выше модель применима для G_e при длине пролета больше чем 20 км. На более коротких пролетах распределение G_e совпадает с распределением G взятом в любой точке пролета (т.к. имеет местный характер).

г) На пролетах протяженностью больше чем 20 км значение G_e, превышающие данный процент времени легко вычисляется путем интегрирования функции гауссовской плотности вероятности с параметрами m _э и s _э. В частности:

(18)

(19)

д) При вычислении m и s необходимо обратить внимание на то, что условия распространения, приводящие к уменьшению просвета характеризуются градиентами большими чем среднее значение G_m. Это учитывается допущением m = G_m и вычислением s из распределения фиктивного градиента, которое совпадает с реальным при G> G_m, в то время как для G< G_m распределение можно получить путем зеркального отображения графика относительно точки абциссы G_m как показано на рис.7.

 

 

 

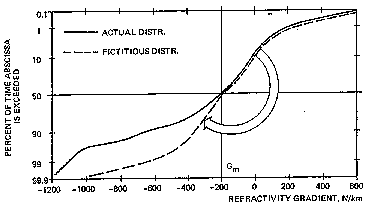
Рис.7 Действительное и фиктивное распределение G.

 

Несколько комментариев относительно полученных выше результатов. Необходимо заметить, что понятие эквивалентного градиента оставляет результаты, полученные в предыдущем разделе правомерными, если произвести замену G на G_e во всех формулах. В частности, выражение (13) будет выглядеть следующим образом:

(20)

Заметим, что Ge имеет меньшую дисперсию чем G, и дисперсия уменьшается с увеличение длинны пролета (17). Физический смысл этого факта в том, что по причине различных метереологических условий на разных участках длинного пролета разные градиенты рефракции, которые могут компенсировать друг друга.

Важное следствие уменьшение величины дисперсии Ge состоит в том, что K также уменьшается, и это уменьшает вероятность того, что K достигнет значений, при которых произойдет потеря прямой видимости.

На правильно спроектированной РРЛ высоты антенн подобраны таким образом, что видимость между антеннами существует даже для самых “низких” лучей, ожидающихся на трассе. На практике берут значение K не превышающие 0.01% времени.

Из (20):

(21)

 

 

 

 

 

 

 

 

 

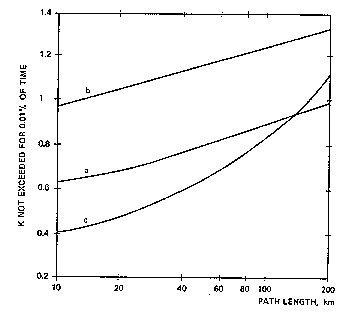
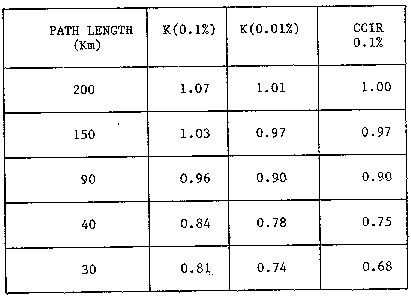
Рис.8 Значения K не превышающие 0.01% времени как функция длинны трассы для следующих типов климата:

График, на рис.8 показывает функциональную зависимость K(0.01%) от длины пролета для трех распределений G, приведенных на рис.1. Заметна довольно большая разница между кривыми, хотя, как и ожидалось, все кривые растут при увеличении длинны пролета. Как видно из таблицы1, хотя значения K по версии МККР даны для 0.1% времени, фактически они взяты из [8], где они обозначены как значения при 0.01% времени. Нетрудно заметить, что эти значения практически совпадают со значениями в третьем столбце для пролетов длинной от 40 до 200 км.

 

 

 

 

 

 

 

 

4. ДИФРАКЦИОННЫЕ ПОТЕРИ.

Когда просвет становится малым, появляются затухание по причине дифракции, и соответственно падает уровень сигнала на приеме. Для определения минимально возможного просвета, при котором еще не появляются потери данного типа рассмотрим понятие первой зоны Френеля, которое имеет важное значение в оценке дифракционных потерь. Интуитивно понятно, и может быть показано, что основная мощность сигнала передается именно в первой зоне Френеля. Следовательно, правомерно ожидать, что закрытие этой области окажет сильное влияние на уровень принимаемого сигнала.

Перед тем, как рассмотреть дифракционные потери в некоторых типичных случаях, оценим размеры первой зоны Френеля вдоль трассы. На расстоянии d1 от передатчика и d2 от приемника:

(22)

Выражение (22) показывает, что F1 зависит как от рабочей частоты, так и от расстояний до передатчика и до приемника. Максимум F1 находится в середине интервала:

(23)

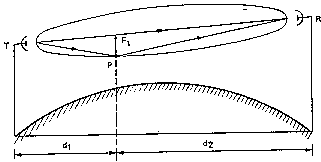
Рис.9 Первая зона Френеля на эквивалентной земной поверхности.

Рассмотрим дифракционные потери как функцию от просвета для трех теоретических типов препятствий: плоской поверхности, гладкой сферической сферы и острого клина. Практический случай лежит где-то посередине. На рис.10 показаны потери в дБ по отношению к потерям в свободном пространстве как функция относительного просвета C=E/F1. Видно, что во всех случаях потери нулевые при C=0.6, и они возрастают при уменьшении С. Скорость возрастания зависит от типа препятствия. В частности, широкое препятствие с хорошо отражающей поверхностью производит большие потери, чем препятствие с меньшими горизонтальными размерами (вершины гор, например) или препятствие с абсорбирующей поверхностью (лес).

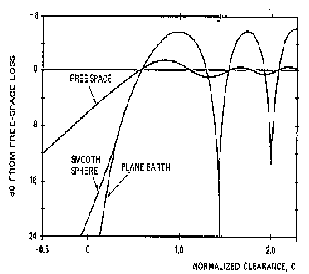
Рис.10 Дифракционные потери на различных типах препятствий.

 

5. ПРАВИЛА ВЫБОРА ПРОСВЕТА.

Практическая проблема при проектировании РРЛ состоит в выборе высот антенн таким образом, чтобы они были не выше, чем минимально необходимые. Для этого необходимо удовлетворить следующим условиям:

1. Вероятность того, что произойдет потеря прямой видимости при аномальных условиях должна быть принебрежима мала.
2. Приемлемые дифракционные потери при нормальных условиях прохождения.

Вот некоторые критерии видимости, используемые до настоящего времени:

а) Просвет должен быть не меньше чем 0.6 первой зоны Френеля при минимальном K.

б) Просвет должен быть равен 1 или больше при K=4/3.

Заметим, что а)- это рекомендация МККР только для умеренного типа климата. Для других типов климата минимум просвета должен быть вычислен по процедуре, описанной в разделе 3. Аналогичное замечание относится и к б) - для других типов климата K=4/3 должно быть заменено средним значением K, определенным из (13) по метереологическим измерениям среднего значения G.

В настоящее время а) и б) несколько видоизменены.

Подход к выбору высот антенн при плохих условиях распространения.

Задача проектировщика - гарантировать, дифракционные потери не превышают запас на замирания (Vmin по методике НИИР) даже в течении пренебрежимо малом процента времени. Согласно МККР:

Недоступность (25)

где d - в км.

Первый шаг при выборе высот антенн - вычисление K(0.01%) по процедуре, описанной в разделе 3. Затем необходимо определить соответствующий относительный просвет C и вычислить появляющиеся при нем потери по графику на рис.10. Эмпирические формулы даны в [7] и [16]. Например следующее выражение может быть использовано для гладкой поверхности:

А= -15+25С (26)

Сопоставляя Vmin и А добиваются того, чтобы высоты антенн были такими, чтобы А=-Vmin. Когда это условие выполнено необходимо немного увеличить высоты антенн для того, чтобы удовлетворить (25) и застраховаться от погрешности построения профилей интервала, возможного роста деревьев и т.п. Например, высоты антенн могут быть увеличены таким образом, чтобы уменьшить в 10 раз недоступность (25) т.е. промежуток времени, в течении которого дифракционные потери превышают Vmin.

В результате а) можно переписать следующим образом:

а’1) Определить высоты антенн, при которых дифракционные потери равны Vmin при K(0.01%).

а’2) Несколько увеличить высоты антенн, чтобы сделать несущественной (сравнимую с (25)) вероятность того, что дифракционные потери превышают запас на замирания.

Подход к выбору высот антенн при нормальных условиях распространения.

После того, как условия a’1) и a’2) выполнены, необходимо проверить просвет при нормальных условиях прохождения. Приемлемая величина просвета - не меньше чем С=0.6. Увеличение просвета практически не увеличивает уровень принимаемого сигнала (см. рис.10), в то время как это влечет за собой увеличение высот подвеса антенн, и как следствие - удорожание строительства.

Для низких частот (1-2 ГГц) где абсолютная величина первой зоны Френеля большое, просвет может быть сделан даже меньше чем C=0.6. Это зависит от стоимости разных компонентов системы. Например, дифракционные потери в 1 дБ могут быть скомпенсированы увеличением мощности передачи на 1 дБ, либо увеличением коэффициента усиления антенн на 1 дБ и т.д.

Таким образом, б) можно заменить на:

б’) Добиться относительного просвета около 0.6 при среднем значении K для данного типа климата.

 

В методике, описанной в руководстве к программе “PathLoss” высоты антенн выбираются следующим образом:

Для определения минимальных высот антенн теперь требуется определить дифракционные потери при минимальном ожидаемом К и связать с пределом теплового затухания для трассы (Vmin). Основная процедура описывается следующими шагами:

1. Вычислить высоты антенн с помощью критерия минимальной видимости при 60%F1 и K=4/3.
2. Вычислить предел теплового затухания Vmin.
3. Определить значение К, которое будет превышаться в течение 99,9% времени.
4. Используя значение К из шага 3, определить высоты антенн, которые приводят к следующим дифракционным потерям:

5. Выбрать максимальные значения высоты антенн, определенные в шагах 1 и 4.

назад      на главную страницу

April 29, 1999
Copyright © 1999 ТелекомПроект
Last modified: